Equipe de Coordination IHM et Affichage 3D Formats d'échanges Optimiseur de données
Thèmes proposés :
Placage de Bitmap Placage de Graphes 2D Toponymie en 3D Bloc Diagramme Orienté Vol à vue furtif Réseaux de fluides Lignes électriques aériennes Tronçons de galeries Bâtiments et toits Placage de cadastre Propagation d'inondation Lit de rivières sur MNT Ecorché géologique Sites souterrains Propagation de pollution Propagation d'incendie Itinéraire sous contraintes Suivi GSM de véhicules BBD photos Simulation discrète sur MNT Croissance végétale
Principes utilisés :
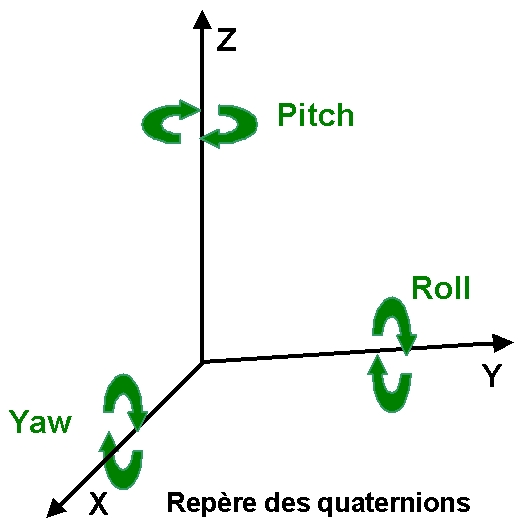
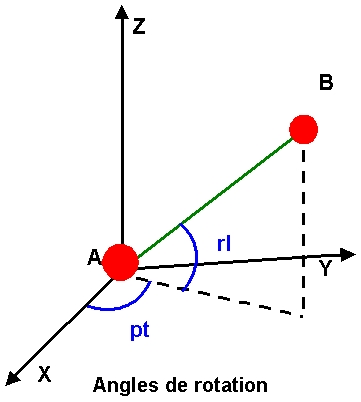
Les quaternions
Multithèmatique :
Exemples d'interfaçage
Liens :
Programmation : Tous les langages. SIG et informatique : emplois, cours, biblio. Formations. Linux : vers le monde du pingouin. Divers : Autres liens.